
|
Lesson Plan 31: Redwood
Trees: How Tall?
First posted May 3, 2004 Last
updated June 19, 2009
This Lesson Plan shows
how to measure the height of a redwood tree
(Grade Level 9-12, but younger students can do it with a bit of help)
Remember these points from the Lesson
Plan Homepage:
(1) These lesson plans are not rigid requirements,
but a starting point for the Nature Counselor's
plan for teaching a particular day's experience.
(2) The activity should be fun and emphasize
active learning on the student's part: ask a
question, don't just state a fact.
(3) You should employ hands-on as much as possible.
(4) Plan each session to also allow time for
making entries in the Nature
Journal. |
Prior to the
session
(1) Review this section and the section on the Redwood
Forest, the World's Tallest Tree, and our trees (Coast
Redwood, Douglas-fir, alder, big leaf maple, tanbark-oak.)
(2) If needed, brush up on your geometry and algebra
as applied to this lesson.
(3) Be sure to have the yardstick and some string.
Session
(1) Start with walking around camp, observing the height
of the various trees that we have. Identify the species.
* What species of trees are at Cazadero? How can you
identify them? Leaves, bark, size, shape?
* Rank the tree species in terms of height. Are some
of the specimens here short, but you can often find
them taller elsewhere? Why?
(2) Redwoods are obviously the tallest trees we have.
* What redwood tree is the tallest? (coast redwood)
What redwood is the most massive? (giant redwood)
Is any redwood deciduous? (dawn redwood)
* Which of the coast redwoods at Cazadero is the tallest?
(3) It might be fun to know how tall our tallest tree
is.
* How could you measure the height of the tallest
tree? How you could make a rough guess? Each student
should independently estimate the height and write
their answer in their Journal.
* Discuss the estimates. Do you want to change yours?
Why?
* How can you make a better guess? (Take an object
of known height, guess how many time taller the redwood
is.) Each student should write their answer in their
Journal.
* Discuss this second estimate. Do you want to change
yours? Why?
* How can you measure it more accurately? If necessary,
ask them to use their geometry knowledge to design
a way to measure a redwood. Another suggestion: If
a person who is six feet tall has a shadow that is
X long, how long would the shadow be at the same time
of a person who is three feet tall? (Answer: 1/2 X.) Does this
give you an idea about how to measure the height of
the redwood tree? Each student should draw their concept
in their Journal. Discuss.
(4) Divide the students into groups of about three
or four. Each group should independently try this step.
Solution: geometry can be used in several ways to
measure the height of a tree. (Don't forget Step 5,
below, when you are finished.)
 |
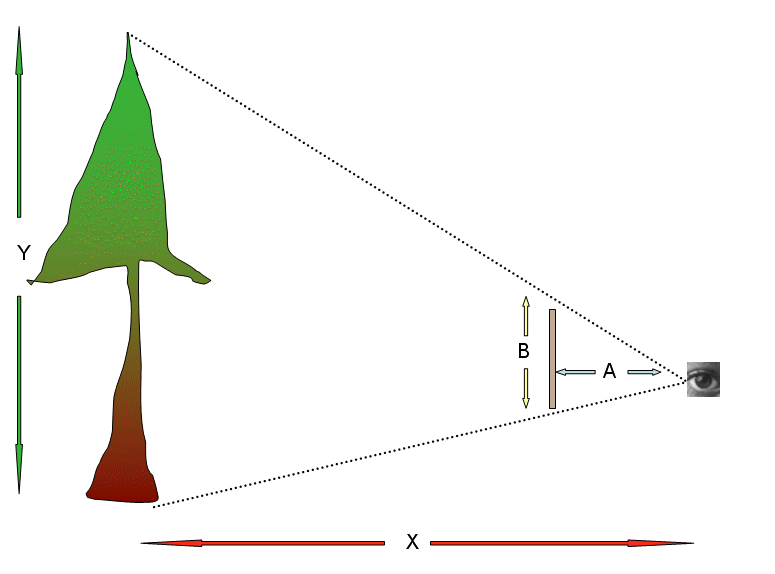
The distance Y is what we want to
determine. The distance from an observer to the
tree is X, which we can measure with the yardstick
or the string (eg, measure out a ten foot piece
and use that to measure the distance). Since we
know that the ratio of A/B is the same as X/Y, if
we use a known A and a known B (yardstick, friend
of known height), and a known X (the distance from the observer to the tree), we can calculate Y. Also, the length
of shadows could be X and A. |
| |
|
 |
In a similar way, if you held up
a yardstick a known distance from your eye, and
looked at the bottom of the tree, then moved the
0 end of the yardstick to lie in your line of
sight, then without moving the yardstick or your
eye, you could see what measurement on the yardstick
was in line with top of the tree. Algebra gives
you the tree height as in the above example.
Even more fun: if X=25 feet, and A=25 inches,
and if B=number of inches in the line of sight,
the tree height (Y) is B feet tall. (If the tree
is too tall, increase X to 50 feet, and then double
the reading B; or if it is still too tall, increase
X to 75 feet and triple the B reading, etc.) When
you use the yardstick in this manner, it is called
a hypsometer. (See the reference below.) |
| |
|
(5) How accurate was your first estimate? Second? The
final one, using geometry? How do you determine or estimate
the accuracy of any measurement? Does the use of the
measurement help to define how accurate it needs to
be? What have you learned about successive approximation?
References
WikiHow has a nice article on measuring the heights of trees, and there are many other websites that have slightly different takes on this common activity. Just Google "measuring the height of a tree/"
Back to the Lesson
Plan Homepage
|

|

